
The 47th Problem of Euclid

(A.K.A. The Pythagorean Theorem)

The problem above is the 47th Problem of Euclid. It is an invention by an ancient Greek geometer, Pythagoras, who worked for many years to devise a method of finding the length of the hypothenuse of a right angle triangle. Pythagoras is credited with having first proved the rule successfully applied to the problem.
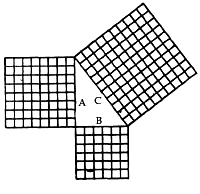
The rule is that the square of the base added to the square of the altitude equals the square of the hypothenuse. The base of a right angle triangle is the side on which it rests, marked B in the Figure above. The altitude is the height and is marked A. The hypothenuse is the connecting side of the triangle, marked C above. The base, 6, squared or multiplied by itself, equals 36. The altitude, 8, squared, equals 64. By adding these together we have 100, which is the square of the hypothenuse. It remains but to extract the square root of 100, which we know is 10, therefore 10 is the length of the hypothenuse or third side of this right angle triangle. All right angle triangles can be figured in the same manner, but only multiples of the length of the three sides come even -- such as 3, 4, 5 and 12, 16, 20, and many others, of course.
Compiled by: Wor.
David J. Lettelier
for a Public Oration and Lecture
The 47th problem of Euclid (called that because Euclid included it in a book of numbered geometry problems) in which the sides are 3, 4, and 5 -- all whole numbers -- is also known as "the Egyptian string trick."
The "trick" is that you take a string and tie knots in it to divide it into 12 divisions, the two ends joining. (The divisions must be correct and equal or this will not work.)
Then get 3 sticks -- thin ones, just strong enough to stick them into soft soil. Stab one stick in the ground and arrange a knot at the stick, stretch three divisions away from it in any direction and insert the second stick in the ground, then place the third stick so that it falls on the knot between the 4-part and the 5-part division. This forces the creation of a 3 : 4 : 5 right triangle. The angle between the 3 units and the 4 units is of necessity a square or right angle.
The ancient Egyptians used the string trick to create right angles when re-measuring their fields after the annual Nile floods washed out boundary markers. Their skill with this and other surveying methods led to the widely held (but false) belief that the Egyptians invented geometry (geo=earth, metry=measuring).
Thales the Greek supposedly picked the string trick up while traveling in Egypt and took it back to Greece. Some say that the Greek mathematician and geometer Pythagoras, described in Masonic lectures as "our worthy brother," also went to Egypt and learned it there on his own. In any case, it was he who supplied the PROOF that the angle formed by the 3 : 4: 5 triangle is invariably square and perfect. It is also said that he actually sacrificed a hecatomb, that is a sacrifice of one hundred bulls, which ranked as the highest kind of religious offering, upon completing the proof.
How is this forty-seventh proposition the foundation of all Masonry, and what was the significance of the problem which led to such a demonstration by the ancient philosopher?
The knowledge contained in this proposition is at the bottom of all systems of measurement and every mechanic at the present day makes use of it consciously or unconsciously, whether it be the land surveyor blocking out a township, or the gardener measuring out his tennis court, or the carpenter calculating the pitch of a roof. He may not know anything about geometry, but the "rule of thumb" by which he works has been deduced from this proposition. To the practical builder the knowledge is invaluable, and if we will carry ourselves back in imagination to a time when this knowledge was still unknown, we will realize that its discovery was an event of great importance in the history of architecture, an epoch-making event to be ranked with such modern discoveries as those of the law of gravitation, wireless TV or telephones, and space travel.
The Discovery of the 47th problem of
Euclid:
Euclid wrote a set of thirteen books, which were called “Elements”. Each book
contained many geometric propositions and explanations, and in total Euclid
published 465 problems. The 47th problem was set out in Book 1, which is
also known as “The Pythagorean Theorem”. Why is it called by both these
names? Although Euclid published the proposition, it was Pythagoras who
discovered it. We learn from the third degree lecture that:
“ This wise philosopher (Pythagoras) enriched his mind abundantly in a
general knowledge of things, and more especially in Geometry, or Masonry. On
this subject he drew out many problems and theorems, and, among the most
distinguished, he erected this, when, in the joy of his heart, he exclaimed
Eureka, in the Greek language signifying, "I have found it," and upon the
discovery of which he is said to have sacrificed a hecatomb. It teaches Masons
to be general lovers of the arts and sciences”.
To the operative mason it affords a means of correcting his square, for if he wishes to test its accuracy he may readily do so by measuring off 3 divisions along one side, 4 divisions along the other, and the distance across must be 5 if the square is accurate. The knowledge of how to form a square without the possibility of error has always been accounted of the highest importance in the art of building, and in times when knowledge was limited to the few, might well be one of the genuine secrets of a Master Mason. The ancient temple builders in the long centuries before Christ were most punctilious in setting their temples due east and west. So exacting were they on this point that there was organized a set of men who, in modern phrase, would be termed experts or specialists, and whose sole duty it was to lay out the foundations of public edifices. They were called, in Egypt, harpedonaptae--meaning rope stretchers. They first laid out the north and south line by observation of the stars and the sun, and their next step was to get the east and west line exactly at right angles. This they secured by stretching a rope north and south divided divided into three parts in the proportion of 3, 4, and 5, (the Egyptian string trick again) fastening down the centre part by pegs, and then swing round the loose ends toward the west until they intersected and a right angled triangle was thus formed. These ancient temple builders, by means of the centre, formed the square, and the centre was a point round which they could not err. Here also is the obvious answer to the question why it is customary at the erection of all stately and superb edifices to lay the foundation stone at the north-east angle of the building.
The question arises, have we anything in our present ritual which might be relative in any way to this method of proving the square or obtaining a right angle without the possibility of error and which may have been connected with the instruction given in purely operative masonry.
The type of triangle most often used to demonstrate the 47th problem in Masonry is not the 3 : 4: 5 but the 1: 1 : square root of 2 form. The square and the cube which are 1 unit on each side are of great symbolic meaning to Masons. Therefore, the bisection of the square into a pair of 1 : 1 : square root of 2 triangles has important Masonic connotations. It is in this form that the Pythagorean theorem is most often visually encountered in Masonry, specifically in the checkered floor and its tessellated border, as a geometric proof on Lodge tracing boards, as the jewel of office for a Past Master, and in the form of some Masonic aprons.
To create a 1:1 square root of 2 right triangle, also known as an isosceles right triangle, you need a compass and a straight edge -- familiar tools to the Craft, of course. On soft ground, use the compass to inscribe a circle. Then use the straight edge to bisect the circle through the center-point marked by the compass. Mark the two points where the bisecting line crosses the circle's circumference. Using the compass again, erect a perpendicular line that bisects this diameter-line and mark the point where the perpendicular touches the circle. Now connect the three points you have marked -- and there is your 1 : 1 : square root of 2 right triangle.
To Freemasons, the first two points -- where you marked the crossing of the bisecting diameter through the circle's circumference -- can also be used to construct two further perpendicular lines. These are the two "boundary" lines of conduct sometimes symbolized on Masonic tracing boards by the Two Saints John and sometimes referred to as indicators of the Summer and Winter Solstices, whereon the feast days of those two saints occur.
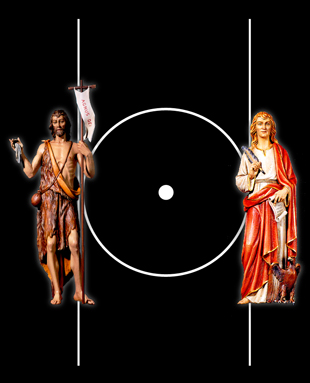
We also have a fragment of great interest in the ceremony of opening the Lodge in the Third Degree. It is from the East and towards the West that one's steps are directed to find that which was lost, and it is with (by means of) the centre, that point round which a Master Mason cannot err. The opening catechism of the Third Degree fits so accurately the process of forming a perfect square as used by the rope stretchers of ancient Egypt that the belief forms in the mind that we have here a fragment of the old operative instruction preserved in the mosaic of speculative Masonry.
No wonder that Pythagoras sacrificed an hecatomb! No wonder that Anderson speaks of this proposition as the foundation of all Masonry! The only wonder is that modern Freemasonry has lost sight of the importance of this symbol.
Our consideration of the subject has brought us back again to the central point of modern Speculative Freemasonry--the knowledge of God--to which all our symbolism points. We seek it in the First Degree under the symbolism of Light; we strive to attain it in the Second Degree as the summit of all knowledge; we learn in the Third Degree that perfect knowledge is not to be attained on this side of the grave; but everywhere it is taught as the unifying bond of the Craft, cementing us as a common brotherhood with a common Father, even God--that God who ever lives and loves, one God, one Law, one element and one far-off divine event to which the whole creation moves.

"The lyf so short, the craft so long to lerne, Th' assay so hard, so sharp the conquering."
-- Chaucer.
![]()